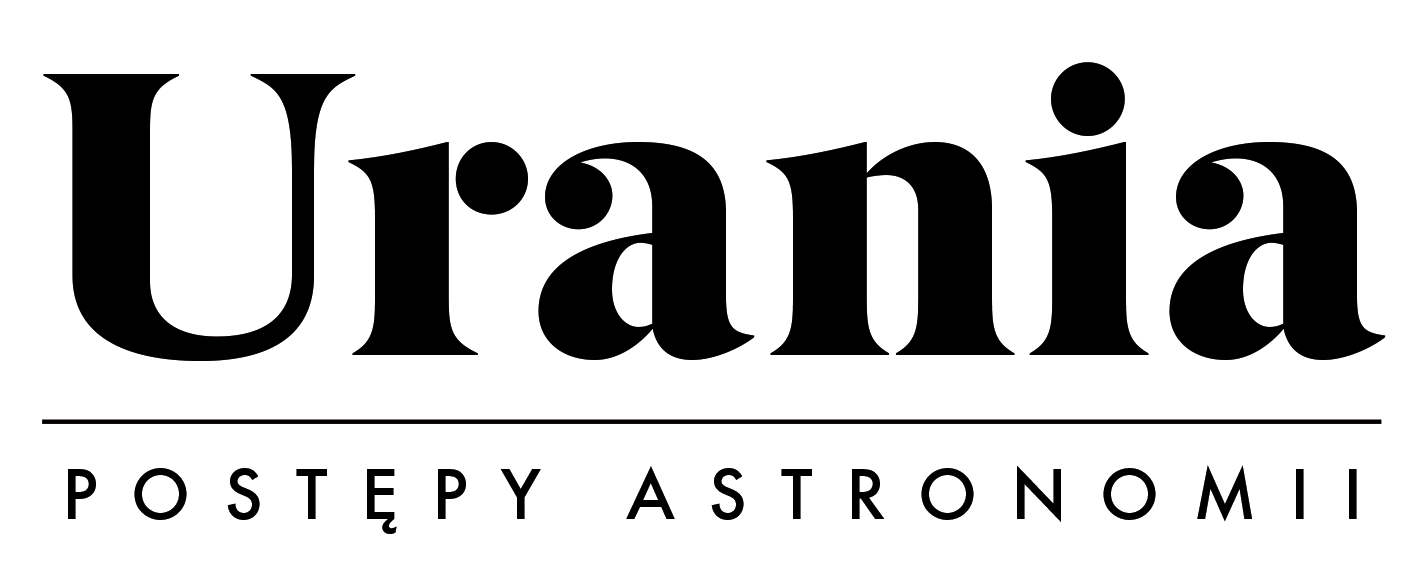Budowa okularu
Cz. II
5
Aberracja chromatyczna powiększenia
Wiązka równoległych promieni światła złożonego, padająca pod kątem na soczewkę sferyczną, po przejściu przez nią utworzy pozaosiowy obraz gwiazdy w postaci wielobarwnego paska. Dzieje się tak, ponieważ promienie fioletowe skupiają się najbliżej osi optycznej soczewki, a dalsze barwy tworzą ogniska coraz dalej od tej osi (rys. 1).
Koma lub astygmatyzm soczewki sferycznej w przypadku światła złożonego, występują razem z aberracją sferyczną i aberracją chromatyczną powiększenia.
6. Krzywizna pola
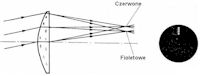
Pozaosiowe obrazy gwiazd nie powstają w płaszczyźnie obrazowej ogniska, lecz na powierzchni wklęsłej (od strony soczewki). W rezultacie w miarę oddalania się od osi optycznej, obrazy gwiazd w płaszczyźnie obrazowej ogniska są coraz bardziej rozmyte (rys. 2).
7. Dystorsja
Obrazy gwiazd w miarę oddalania się od osi optycznej powstają w coraz mniejszej od niej odległości, niż by to wynikało z kierunku padania wiązki światła na soczewkę. W rezultacie odwzorowanie odległości kątowych między gwiazdami nie jest prawidłowe, a pozaosiowe obrazy linii prostych są krzywymi (rys. 3).
Jak wynika z powyższych opisów, obraz gwiazdy utworzony przez soczewkę jest zdeformowany przez kilka aberracji jednocześnie. Interpretacja geometryczna takiego obrazu jest bardzo skomplikowana i dość sztuczna. Trzeba zawsze pamiętać o falowej naturze tego zjawiska. Teoretyczny, punktowy obraz świetlny ma zawsze postać krążka dyfrakcyjnego, a jego zniekształcenia aberracyjne mają charakter interferencyjny.
Pojedyncza soczewka ma szereg wad i jako okular nie jest używana. Bodajże największym jej mankamentem jest aberracja chromatyczna powiększenia. Zniekształca ona bardzo pozaosiowe obrazy gwiazd. Częściową redukcję wad pojedynczej soczewki można uzyskać zmniejszając drastycznie jej światłosiłę.
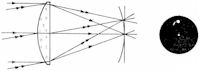
Niestety, okular z takiej soczewki ma niewinietowane pole widzenia praktycznie równe zeru (rys. 4a), co czyni go nieprzydatnym do obserwacji.
Problem ten był zawsze zmorą pierwszych konstruktorów instrumentów astronomicznych. Rozwiązanie jego okazało się genialnie proste. Otóż okazuje się, że jeżeli dwie soczewki z jednakowego gatunku szkła umieścimy w odległości od siebie równej połowie sumy ich ogniskowych, to układ taki jest praktycznie wolny od aberracji chromatycznej powiększenia. Bardzo znacznie są zredukowane również inne wady charakterystyczne dla pojedynczej soczewki. Walory takiego układu wydatnie polepsza zastosowanie w nim soczewek płasko – wypukłych. Soczewki takie są obarczone stosunkowo najmniejszą aberracją sferyczną. Odległość między soczewkami w omawianym układzie, wynikająca z warunku jego achromatyczności, określa następująca formuła:
![]() (1)
(1)
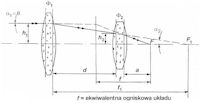
Podstawowe parametry dwusoczewkowego układu optycznego, ukazane na rys. 5, możemy obliczyć przy pomocy następujących zależności matematycznych:
![]() (2)
(2)
lub
![]() (3)
(3)
![]() (4)
(4)
lub
![]() (5)
(5)
![]() (6)
(6)
![]() (7)
(7)
lub
![]() (8)
(8)
Najprostszym okularem dwusoczewkowym o konstrukcji opartej na warunku achromatyczności z wzoru (1), jest okular Ramsdena. Klasyczny okular tego typu składa się z dwu płasko – wypukłych soczewek o takiej samej ogniskowej, ustawionych stronami wypukłymi do siebie, w odległości równej ogniskowej pojedynczej soczewki (rys. 4b). Zgodnie ze wzorem (2), ekwiwalentna ogniskowa takiego układu optycznego równa jest ogniskowej pojedynczej soczewki tego układu.
Lucjan Newelski