Oprawa lustra głównego
Cz. I
Ważnymi elementami konstrukcji teleskopu są oprawy części optycznych. W przypadku teleskopu zwierciadlanego problemów technicznych dostarcza zamocowanie lustra głównego. Ma ono dosyć duże rozmiary i znaczny ciężar. Zwierciadło w oprawie musi zachowywać stały kierunek swej osi optycznej względem pozostałych elementów optycznych teleskopu, nie może zmieniać w istotny sposób swego kształtu, a jednocześnie musi jak gdyby „pływać” na podporach. Szkło jest stosunkowo sztywnym materiałem, ale narzucone przez falową naturę światła warunki zachowania kształtu powierzchni zwierciadła, są bardzo ostre.
Doświadczony szlifierz, miłośnik astronomii, potrafi nadać
powierzchni odbijającej zwierciadła bardzo precyzyjny kształt. Na
przykład, jeśli odchyłka frontu fali świetlnej odbitej od zwierciadła
nie przekracza λ/10 to sama powierzchnia odbijająca jest obarczona błędem dwa razy mniejszym: λ/20 co odpowiada 0.000028 mm dla λ = 0.00056 (światło zielone).
Oprawa zwierciadła musi zapewnić zachowanie tej dokładności. Uginanie się lustra pod własnym ciężarem powinno być znikomo małe. Traktując zwierciadło jako ciało doskonale sztywne, wystarczy podeprzeć je w trzech punktach symetrycznie rozłożonych pod nim. Ciałem takim zwierciadło jednak nie jest. Jako płyta szklana posiada ono pewną elastyczność, tym większą, im mniejsza jest jego grubość w stosunku do średnicy. Jeśli lustro ma niewielką średnicę i jest odpowiednio grube, to podparcie na trzech punktach jest zupełnie wystarczające. Jednak w miarę zwiększania rozmiarów zwierciadła, a tym samym jego ciężaru, konieczne staje się zwiększenie liczby podpór.
Liczbę koniecznych podpór i ich rozmieszczenie dla zwierciadła w zależności od jego rozmiarów, grubości i rodzaju szkła, ustala tzw. „Reguła Coudera”, określająca stopień ugięcia cylindrycznej płyty szklanej w danych warunkach. D. Maksutow podaje następującą wersję tej reguły:
![]() (1)
(1)
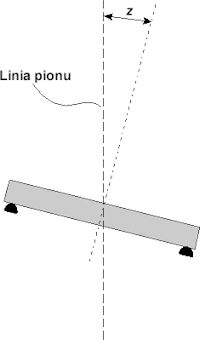
gdzie: D — średnica zwierciadła, h — grubość zwierciadła, d — gęstość szkła, E — moduł Younga dla danego szkła, z — to kąt między kierunkiem pionu, a osią symetrii zwierciadła (rys. 1). Współczynnik K zależy od sposobu podparcia zwierciadła i zastosowanego systemu jednostek.
Człon d/E charakteryzuje mechaniczne właściwości zwierciadła, a (D4/h2)
określa jego geometryczną sztywność przy danych rozmiarach, sposobie
podparcia i nachylenia do pionu. Można powiedzieć, że określona zostaje w
ten sposób wspomniana elastyczność zwierciadła.
Przy konkretnych obliczeniach wygodnie posłużyć się zmodyfikowaną postacią wzoru (1):
![]() (2)
(2)
gdzie symbol σ też określa sztywność zwierciadła z tym, że σ = 1 jest tu wartością graniczną. Dla σ < 1 zwierciadło jest zbyt cienkie dla danego sposobu podparcia, a dla σ > 1 zwierciadło posiada odpowiedni zapas sztywności. Cn spełnia tę samą rolę co K w równaniu (1) z tym, że wartości Cn
zostały ustalone doświadczalnie na podstawie badań przeprowadzonych
przez A. Coudera. Rozpatrując najmniej korzystne ustawienie zwierciadła
przy z = 0 i kładąc σ = 1 znajdujemy hmin ze wzoru (2), czyli minimalną grubość lustra przy danym sposobie podparcia:
![]() (3)
(3)
Ze względu na rozmiary zwierciadeł stosowanych w teleskopach amatorskich, wystarczy rozpatrzyć podparcie na 3, 6, 9 i 18 punktach. Odpowiednie współczynniki Cn są następujące:
![]()
Są one tak dobrane, by nie nastąpiło zauważalne pogorszenie jakości obrazów gwiazd, wywołane uginaniem się szkła. Dla Pyrexu d = 2.25, E = 6200. D i h są w milimetrach.
Wstawiając te wartości do wzoru (3), możemy ułożyć tabelki z D i h minimalnym:
Dla 3 punktów:
![]()
| D | 50 | 60 | 80 | 100 | 150 | 200 | 250 |
| hmin | 50 | 60 | 80 | 100 | 150 | 200 | 250 |
Dla 6 punktów:
![]()
| D | 150 | 200 | 250 | 300 | 350 | 400 | 450 |
| hmin | 6 | 10.6 | 16.5 | 23.8 | 32.5 | 42.3 | 53.6 |
Dla 9 punktów:
![]()
| D | 250 | 300 | 350 | 400 | 450 | 500 | 550 |
| hmin | 14 | 19.8 | 27 | 32.5 | 44.6 | 55 | 66.6 |
Dla 18 punktów:
![]()
| D | 400 | 450 | 500 | 550 | 600 | 650 | 700 |
| hmin | 13.6 | 17.3 | 21.3 | 25.8 | 30.7 | 36 | 41.7 |
W przypadku szkła typu Kron, które jest cięższe od Pyrexu, jego gęstość i moduł Younga wynoszą odpowiednio: d = 2.53, E = 7000. Formuły na hmin będą następujące:
![]() (3 punkty),
(3 punkty),
![]() (6 punktów),
(6 punktów),
![]() (9 punktów),
(9 punktów),
![]() (18 punktów),
(18 punktów),
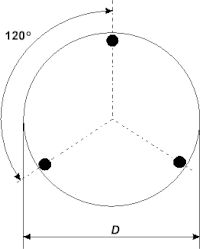
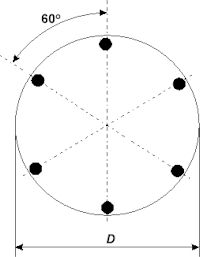
Punkty podparcia, na których zwierciadło spoczywa, muszą być rozmieszczone w określony sposób. Przy podparciu w 3 i 6 punktach, miejsca podparcia mogą być rozmieszczone blisko krawędzi płyty zwierciadła, co 120 lub 60 stopni względem jego środka (rys. 2 i 3). Jeśli punktów podparcia jest 9 lub 18,
sposób rozmieszczenia jest bardziej skomplikowany. Stosowną metodę
podał J.H. Hindle. Polega ona przede wszystkim na ustaleniu tzw. okręgów
równowagi — (ang. radii of equilibrium), na których są umieszczone punkty podparcia.
Lucjan Newelski
Tomasz Krzyt