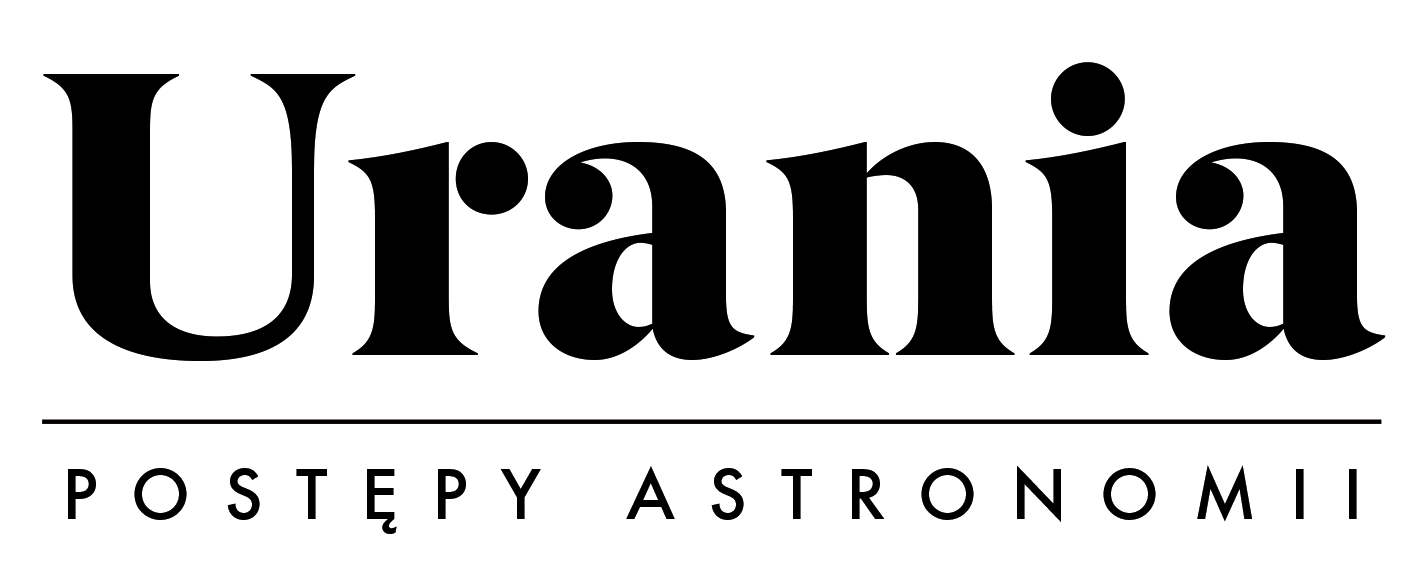Fizyczne zjawisko fali stojącej jest nam dobrze znane z życia codziennego oraz z mechaniki i elektromagnetyzmu, gdzie fala taka posiada maksymalną i minimalną amplitudę odpowiednio w swoich węzłach i antywęzłach. Teraz astrofizycy z Uniwersytetu Jagiellońskiego w Krakowie przeanalizowali model czasoprzestrzeni zawierającej stojące fale grawitacyjne w rozszerzającym się Wszechświecie – w kontekście rozwiązania równania pola Einsteina.
Ogólna teoria względności Alberta Einsteina opisuje grawitację jako swoistą geometrię samej czasoprzestrzeni. Trzy wymiary przestrzenne i jeden wymiar czasowy, które składają się na czasoprzestrzeń, w której żyjemy, stały się w tej teorii niej bytem aktywnym i dynamicznym. To bardzo ważne, bowiem wcześniej, w dynamice newtonowskiej, podstawowe oddziaływania i prawa fizyczne rozgrywały się w nieruchomej czasoprzestrzeni – stanowiła ona tam jedynie scenę w tle, pewnego rodzaju dekorację, a głównymi bohaterami spektaklu były niezmiennie cząsteczki i pola oddziaływań. Pomysł Einsteina zrewolucjonizował to podejście – w ogólnej teorii względności (1907–1915) i późniejszych badaniach nad grawitacją to także sama czasoprzestrzeń (przestrzeń i czas) są dynamicznymi, aktywnymi uczestnikami wszystkich wydarzeń.
W OTW siła grawitacji wynika z lokalnej geometrii czasoprzestrzeni. Aparat matematyczny tej teorii opiera się na różniczkowym ujęciu geometrii stworzonym przez Gaussa, Riemanna, Christoffela, Ricciego oraz Levi-Civitę. Zastosowanie metod geometrii nieeuklidesowej w fizyce zapoczątkował Hermann Minkowski, który w 1907 roku w pewnym sensie sformułował szczególną teorię względności Einsteina (STW) w języku geometrii, po raz pierwszy wprowadzając pojęcie czterowymiarowej przestrzeni (czasoprzestrzeń Minkowskiego).
Czym są jednak fale stojące? Możemy je tak naprawdę zobaczyć na własne oczy. Gdy szybko i nagle wprawimy w ruch sznurek przywiązany do ściany lub szarpniemy za strunę gitary, pojawią się fale, których grzbiety i doliny (maksima i minima) nie przemieszczają się wzdłuż sznurka czy struny. Fala stojąca powstaje na skutek interferencji dwóch podobnych fal poruszających się w tym samym kierunku, lecz o przeciwnych zwrotach. W praktyce pojawiają się najczęściej wtedy, gdy na propagującą się w przód falę nakłada się taka sama fala odbita.
We współczesnej teorii grawitacji istnieją z kolei zupełnie inne zmarszczki czasoprzestrzeni – wykryte kilka lat temu fale grawitacyjne. Można więc zadać sobie pytanie, czy istnieją też stojące fale grawitacyjne (nakładające się na siebie fale grawitacyjne)? Dokładniej: czy równania pola Einsteina dopuszczają takie rozwiązanie, które można interpretować jako stojącą falę grawitacyjną? Wiemy już, że da się nałożyć na siebie dwie fale elektromagnetyczne (np. światło), ponieważ leżąca u ich podstaw teoria – elektromagnetyzm – jest teorią liniową. Jednak już ewentualna superpozycja, czyli nakładanie się na siebie dwóch fal grawitacyjnych, byłaby znacznie bardziej skomplikowana ze względu na nieliniową naturę grawitacji (równania OTW są nieliniowe).

Na ilustracji: Symulacja łączenia się czarnych dziur – zjawiska, które wytwarza jedne z najsilniejszych fal grawitacyjnych. Źródło:
Okazuje się jednak, że w pewnych warunkach naukowcy mogą badać model Kosmosu znany jako czasoprzestrzeń Gowdy'ego, reprezentujący właśnie nieliniową superpozycję fal grawitacyjnych. Uczeni z Obserwatorium Astronomicznego Uniwersytetu Jagiellońskiego przeanalizowali w tym przypadku uproszczony model zabawkowy, przedstawiający rozszerzający się Wszechświat wypełniony falami grawitacyjnymi, które oddziałują ze sobą, generując tym samym stojące fale grawitacyjne. Geometria tej 4-wymiarowej czasoprzestrzeni ma przekroje przestrzenne o topologii torusa. Innymi słowy, jest to trójwymiarowy torus, który możemy sobie wyobrażać jako pączek (donut), ale w wyższym wymiarze. Zamiast łączyć ze sobą przeciwległe boki kwadratowej płytki, tworząc w ten sposób dwuwymiarowy torus, łączymy przeciwległe strony sześcianu, uzyskując torus w trzech wymiarach. Rysunek 1 pokazuje, w jaki sposób możemy badać fale stojące w podobnym torusie dwuwymiarowym. Podstawowym celem zespołu było uzyskanie rodziny obserwatorów w czasoprzestrzeni, której geometria przestrzenna ma topologię torusa trójwymiarowego, i zrozumienie, jak zachowywałyby się w niej swobodnie spadające masy (cząstki) próbne.
Stojące fale grawitacyjne w tak zdefiniowanej czasoprzestrzeni rozchodzą się w kierunku Z. Okazuje się, że w tym kierunku obecne tam cząstki próbne są przyciągane do antywęzłów fali. Można sobie wyobrazić, że skoro amplituda fali jest maksymalna na antywęzłach, to właśnie w nich koncentruje się energia grawitacyjna. Oznaczałoby to obecność źródła potencjału grawitacyjnego, działającego jako obszar przyciągania cząstek. Właśnie to odkryto w badanym modelu czasoprzestrzeni – statystycznie rzecz biorąc, cząstki próbne są przyciągane przez antywęzły. Okazuje się też, że obecny tam pierścień mas próbnych zostaje trwale odkształcony w kierunku poprzecznym. Ten trwały efekt, pozostały po przejściu fali grawitacyjnej, znany jest też jako pamięć fal grawitacyjnych.
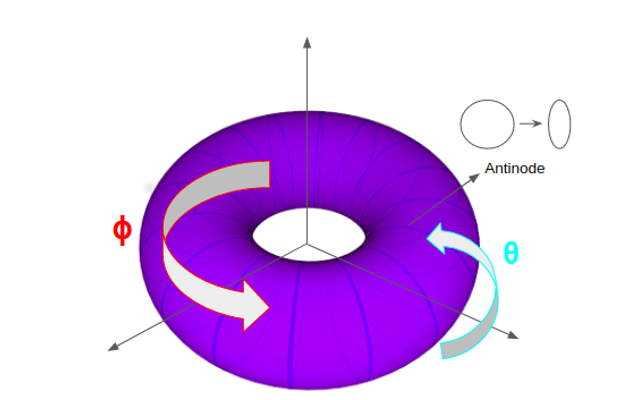
Ale to nie wszystko. Fale grawitacyjne wykrywane od niedawna na Ziemi mają pochodzenie astrofizyczne. Są generowane przez zwarte obiekty (takie jak czarne dziury czy gwiazdy neutronowe) znajdujące się bardzo daleko od Ziemi. Natura tych wykrywanych fal grawitacyjnych ma charakter poprzeczny. W ogólności zachodzą też jednak dodatkowe efekty podłużne i kulombowskie, które są słabo widoczne, gdy zwarty obiekt generujący fale jest bardzo odległy. Jeśli fala grawitacyjna propaguje się w kierunku Z, to zachodzą łącznie aż trzy różne efekty: poprzeczny (ściśnięcie pierścienia cząstek w kierunku XY do postaci elipsy), podłużny (ściśnięcie pierścienia w kierunku Z, również do elipsy) i tzw. kulombowski, polegający na zgnieceniu kuli cząstek w kierunku Z do postaci elipsoidy.
Przestrzeń, którą badano, zawiera jednak jedynie fale grawitacyjne. Z tego powodu można w niej szukać również tych dodatkowych efektów. W ramach omawianej pracy znaleziono też efekt kulombowski dla stojącej fali grawitacyjnej. Kula mas próbnych w tej czasoprzestrzeni zostaje zgnieciona i przekształcona w elipsoidę obrotową, w kierunku propagacji fali. Ilustruje to Rysunek 2 .
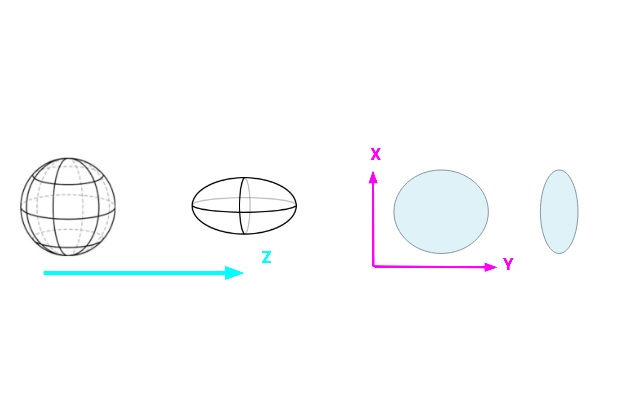
Rysunek 2. Co zobaczy rodzina obserwatorów w przestrzeni Gowdy'ego? Po lewej: sfera mas próbnych odkształcająca się w elipsoidę w kierunku propagacji fali. Po prawej: po pewnym czasie pierścień cząstek zostaje trwale odkształcony w elipsę w kierunku poprzecznym. Źródło: Publikacja zespołu.
Analizowana przez naukowców czasoprzestrzeń z falami grawitacyjnymi jest jedynie modelem uproszczonym. Mimo to wykryte przyciąganie cząstek do antywęzłów i efekt podłużny oraz kulombowski faktycznie wskazują na obecność nieliniowych efektów grawitacyjnych, których można się spodziewać po nałożeniu na siebie fal grawitacyjnych. Przyszłe badania będą dotyczyły tego, w jaki sposób fala elektromagnetyczna sprzęga się z grawitacją i jaka jest natura cząstek w takiej czasoprzestrzeni.
Czytaj więcej:
- Oryginalna publikacja: Freely-falling bodies in standing-wave spacetime; Sebastian J. Szybka, Syed U. Naqvi, Phys. Rev. D 103, 024011, 6 January 2021.
- Zakład Astrofizyki Relatywistycznej i Kosmologii Obserwatorium Astronomicznego Uniwersytetu Jagiellońskiego.
Źródło: OAUJ
Opracowanie: Syed U. Naqvi, Elżbieta Kuligowska
Na ilustracji: Dwuwymiarowy torus, w którym fala stojąca jest skierowana w kierunku ϕ. Antywęzły powstają w niebieskich okręgach w płaszczyźnie θ. W płaszczyźnie θ można badać poprzeczną naturę fal grawitacyjnych, natomiast w kierunku ϕ – podłużną. Zbadaliśmy czasoprzestrzeń, w której wymiary przestrzenne reprezentuje torus trójwymiarowy. Na jego antywęzłach znaleziono trwale zdeformowany pierścień cząstek, co wskazuje na efekt pamięci fal grawitacyjnych. Źródło: https://www.einstein-online.info/en/spotlight/gowdy_st/.