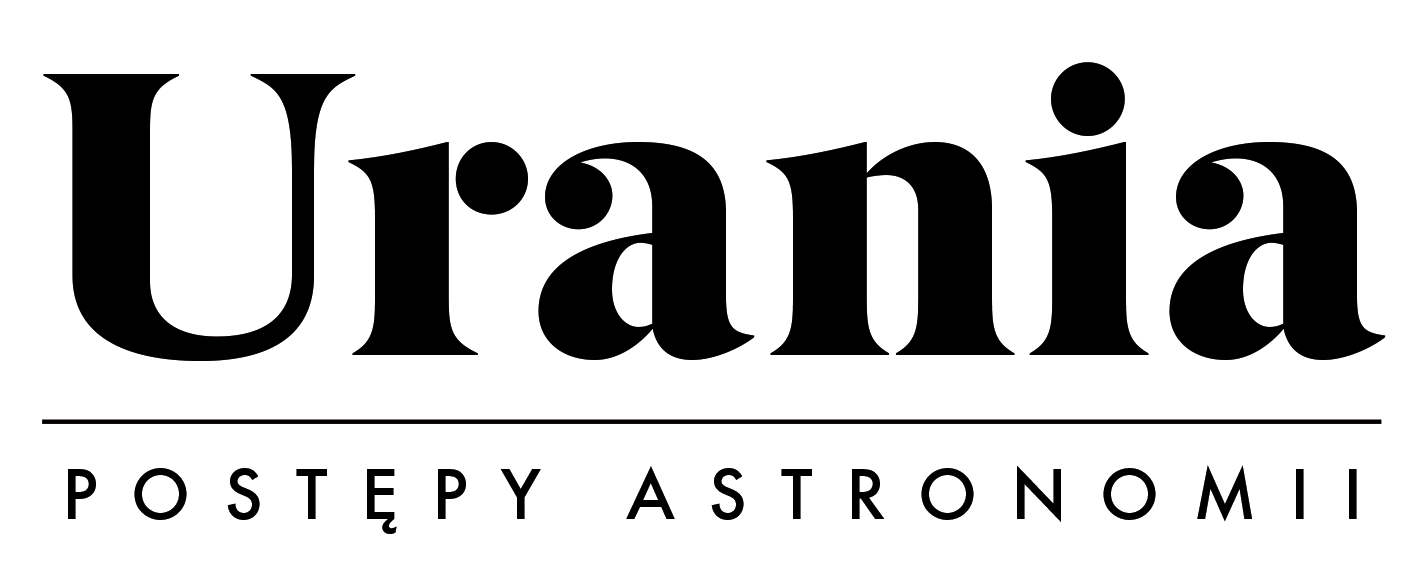Budowa okularu
Cz. I

Rys. 1

Ważną częścią wyposażenia teleskopu są okulary, które są niezbędne przy prowadzeniu obserwacji wizualnej. Okular jest elementem optycznym biorącym równorzędny udział w tworzeniu obrazu gwiazdy na siatkówce oka. Pośredniczy on między obrazem utworzonym przez obiektyw w ognisku głównym teleskopu, a soczewką w oku obserwatora. Niektóre najprostsze typy okularów mogą być wykonane w zakresie amatorskim. Okulary te składają się z dwóch pojedynczych soczewek, których to budową i zasadą działania obecnie się zajmiemy.

Przy ukośnym przechodzeniu czoła fali świetlnej przez gładką powierzchnię bryły szklanej, kierunek ruchu fali ulega zmianie. Dzieje się tak, ponieważ prędkość poruszania się światła w szkle (około 200 000 km/s) jest mniejsza niż w powietrzu i część czoła fali świetlnej będąca już we szkle, porusza się wolniej od części biegnącej jeszcze na zewnątrz niego. W rezultacie fala skręca (rys. 1). Mówiąc językiem optyki geometrycznej, promień świetlny przechodząc z powietrza do szkła (lub odwrotnie), ulega załamaniu na granicy tych dwóch ośrodków.

Rys. 2

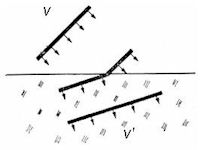
Kąt i między prostopadłą do powierzchni załamującej, a promieniem padającym nazywa się kątem padania, kąt i' między prostopadłą, a promieniem załamanym — kątem załamania (rys. 2).

Wzajemne zależności między tymi kątami określa prawo załamywania się światła, które brzmi następująco:

1. promień padający, prostopadła w punkcie padania i promień załamany leżą w jednej płaszczyźnie;
2. stosunek sinusa kąta padania do sinusa kąta załamania jest dla dwu różnych środowisk wielkością stałą i równa się stosunkowi prędkości światła w środowisku promienia padającego, do prędkości światła w środowisku promienia załamanego

Rys. 3

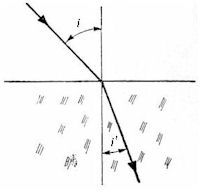
Zjawisko załamywania się światła wykorzystujemy do tego samego celu, co jego odbijanie się w obiektywie zwierciadlanym. Na drodze fali świetlnej ustawiamy tak ukształtowaną bryłę szklaną, że płaskie czoło fali po przejściu przez nią przybierze kształt sferyczny. Bryła taka stanie się wtedy obiektywem. Przynajmniej jedna z powierzchni tej bryły musi być hiperboloidą lub elipsoidą. Druga powierzchnia może być płaszczyzną — lub sferą. Stosowane są soczewki hiperboloidalne – płaskie lub elipsoidalne – sferyczne (rys. 3). Łatwo zauważyć, że w pierwszej soczewce pierwsza powierzchnia, a w drugiej soczewce druga — nie biorą udziału w załamywaniu światła.

Soczewki te będą spełniały to samo zadanie co zwierciadło paraboloidalne, z jednym zastrzeżeniem: każda taka soczewka będzie prawidłowo działać tylko przy fali świetlnej o jednej określonej długości. Powodem tego jest różna prędkość we szkle fal świetlnych o różnej długości. Na przykład światło fioletowe porusza się wolniej od światła czerwonego i tym samym jego współczynnik załamania jest większy niż dla czerwieni.

Rys. 4

Wykonanie soczewek o opisanych kształtach jest bardzo trudne, a przy małych ich rozmiarach wręcz niemożliwe. W praktyce stosujemy soczewki o obu powierzchniach sferycznych lub o jednej powierzchni sferycznej i jednej płaskiej (rys. 4). Dla wykonawstwa amatorskiego praktycznie dostępne są tylko soczewki płasko – wypukłe. Stopień trudności przy ich wykonaniu jest najmniejszy. Z takich to właśnie soczewek składają się dwa podstawowe i zarazem najprostsze typy okularów — Ramsdena i Huygensa.

Rys. 5

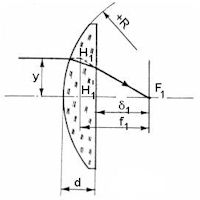
Podstawowymi wielkościami technicznymi soczewki płasko – wypukłej są: promień krzywizny jej powierzchni sferycznej R, jej największa grubość d oraz współczynnik załamania n dla szkła, z którego jest wykonana (rys. 5).

Z tych wielkości wynikają parametry optyczne soczewki. Promień świetlny biegnący równolegle do osi optycznej soczewki i padający na nią w odległości y od tej osi, przechodzi kolejno przez powierzchnię sferyczną i płaską, ulega przy tym dwukrotnemu załamaniu i przecina oś optyczną w punkcie F₁. Punkt ten jest pierwszym ogniskiem soczewki. Jeżeli przedłużymy do wewnątrz soczewki promień padający i promień wychodzący, to przetną się one w punkcie H₁. Rzut tego punktu na oś optyczną jest punktem H₁'. Jest to pierwszy główny punkt soczewki. Odległość między punktami H₁' i F₁ przy y nieskończenie małym, jest pierwszą odległością ogniskową soczewki f₁, a odległość soczewki od punktu F₁ jest pierwszą odległością ogniska od soczewki S₁.

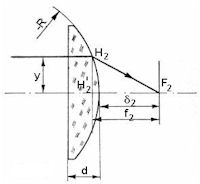
Przy odwrotnym ustawieniu soczewki, drugi punkt główny soczewki H₂' leży na wierzchołku powierzchni sferycznej, a druga odległość ogniskowa soczewki f₂ jest równa drugiej odległości ogniska S₂ od soczewki (rys. 6).

Rys. 6