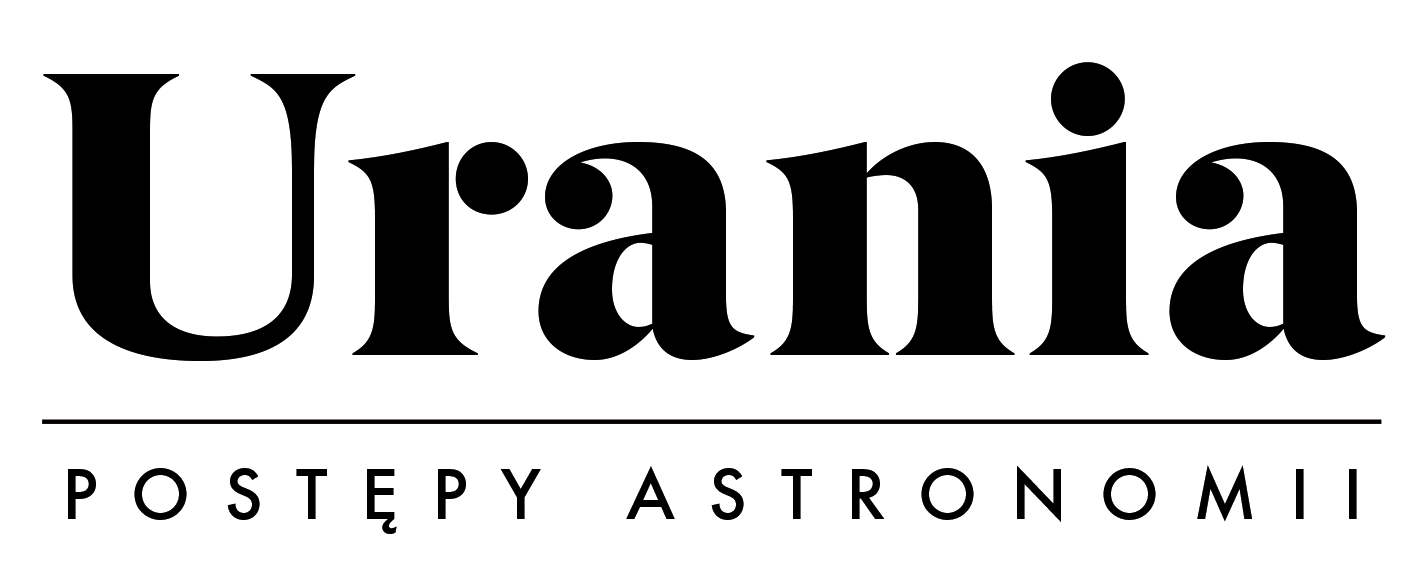Teleskop Newtona
Cz. III
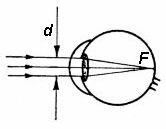 Rys. 1
Rys. 1
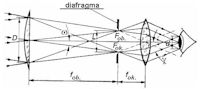
Biegnąca od gwiazdy wiązka światła wpada do źrenicy oka i, po przejściu przez soczewkę w oku, skupia się na siatkówce, tworząc na niej obraz gwiazdy rejestrowany przez nasz zmysł wzroku (rys. 1). Warunkiem rejestracji jest odpowiednio wystarczająca jasność tego obrazu, a co za tym idzie odpowiednia ilość energii świetlnej wpadającej do oka. Budowa źrenicy oka z góry narzuca nam szerokość wpadającej do niego wiązki światła. Jeżeli jasność gwiazdy będzie zbyt mała, natężenie światła w tej wiązce będzie za małe, aby wytworzyć wystarczająco jasny obraz tej gwiazdy na siatkówce. Możemy jednak to natężenie w przypadku każdej gwiazdy zwiększyć. W tym celu stosujemy do obserwacji wizualnych układ optyczny zwany „układem teleskopowym” (rys. 2). Składa się on z obiektywu i sprzężonego z nim na wspólnej osi optycznej okularu. Najprostszym okularem jest pojedyncza krótkoogniskowa soczewka dodatnia. Głównym zadaniem układu teleskopowego jest zwężenie wiązki promieni równoległych padających na obiektyw, do średnicy równej lub mniejszej od źrenicy oka, bez zmiany ilości energii świetlnej w tej wiązce.
Ilość światła padająca od danej gwiazdy na obiektyw lub do źrenicy
nieuzbrojonego oka, jest proporcjonalna do ich powierzchni lub kwadratu
ich średnic. Źrenica ludzkiego oka może w skrajnie optymalnych warunkach
osiągnąć średnicę 0.8 cm. Możemy wtedy dojrzeć nieuzbrojonym okiem gwiazdy 6.2 wielkości. Zysk w ilości odebranego światła przy użyciu teleskopu możemy wyrazić w następujący sposób:
![]() (1)
(1)
Skok o jedną wielkość gwiazdową odpowiada 2.5– krotnej zmianie ilości odbieranego przez nas światła. Wobec czego możemy napisać:
![]()
skąd:
![]() (2)
(2)
Wzór ten podaje teoretyczny wizualny zasięg teleskopu w zależności od średnicy jego obiektywu (w cm).
Jest on słuszny dla idealnego instrumentu i idealnych warunków
obserwacji. W praktyce wizualny zasięg teleskopu jest zawsze nieco
mniejszy. Dla ułatwienia orientacji służy tabela I.
| D (w mm) | 50 | 60 | 80 | 100 | 150 | 200 | 250 | 300 | 350 | 500 |
| m | 10.2 | 10.6 | 11.2 | 11.7 | 12.6 | 13.2 | 13.7 | 14.0 | 14.4 | 15.2 |
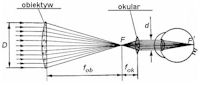
Padające na obiektyw pod kątem ω
do osi optycznej dwie wiązki równoległych promieni świetlnych od dwóch
gwiazd, utworzą w płaszczyźnie obrazowej obiektywu obrazy tych gwiazd,
leżące na brzegu pola widzenia ograniczonego diafragmą okularu (rys. 3).
W dalszym swym biegu wiązki te po przejściu przez soczewkę okularu znów
będą wiązkami promieni równoległych. Średnica wiązek będzie wynosiła d i będą one przecinały oś optyczną pod kątem γ.
W miejscu tego przecięcia umieszczamy źrenicę oka. W rezultacie dwie
gwiazdy leżące na sferze niebieskiej w odległości kątowej 2ω, oko nasze przy użyciu teleskopu widzi pod kątem 2γ. Efekt ten jest kątowym powiększeniem teleskopu, które wyrażamy następującym wzorem:
![]() (3)
(3)
Przy dostatecznie małych kątach można przyjąć:
![]() (4)
(4)
Słuszne są też dwa inne wzory:
![]() (5)
(5)
i
![]() (6)
(6)
Średnica obiektywu D nazywana jest inaczej źrenicą wejściową, a średnica d wiązki wychodzącej z okularu — źrenicą wyjściową. Kątowe wizualne pole widzenia teleskopu 2ω jest tzw. „obiektywnym polem widzenia”, natomiast kąt 2γ jest kątowym polem widzenia okularu i nazywa się „subiektywnym polem widzenia”.
Obiektywne i subiektywne pole widzenia ujmują następujące wzory:
![]() (7)
(7)
i
![]() (8)
(8)
Wygodny w użyciu jest wzór przybliżony:
![]() (9)
(9)
Jednosoczewkowy okular ze względu na liczne wady nie jest stosowany. Najprostsze okulary będące w użyciu mają co najmniej dwie soczewki. Subiektywne pole widzenia jest dla każdego typu okularu znormalizowane i ma wartość stałą.
Ważnymi parametrami teleskopu są jego graniczne powiększenia: minimalne i maksymalne.
Powiększenie minimalne jest to takie powiększenie, przy którym średnica źrenicy wyjściowej jest równa średnicy źrenicy oka. Widać od razu, że jest to uzależnione od warunków obserwacji (w przypadku gwiazd głównie od jasności tła nieba) i od cech fizjologicznych samego obserwatora. Możemy to ująć następującym wzorem:
![]() (10)
(10)
Najbardziej optymalną górną granicą jest powiększenie, przy którym źrenica wyjściowa ma średnicę 0.7 mm.
Rozmiary dyfrakcyjnego obrazu gwiazdy na siatkówce są wtedy na tyle
duże, że możemy dobrze rozróżnić jego detale. Powiększenie to jest
nazywane „powiększeniem rozdzielczym”.
![]() (11)
(11)
Ogniskowa okularu dającego powiększenie rozdzielcze wynosi:
![]() (12)
(12)
Dalsze zwiększanie powiększenia nic nowego nie wnosi, a jedynie pogarsza warunki obserwacji.
Lucjan Newelski